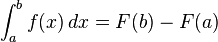ประวัติของแคลคูลัส
ต้นกำเนิดของแคลคูลัสเชิงปริพันธ์ย้อนไปถึงยุคกรีกโบราณ
ยูโดซัส มักจะเป็นที่รู้จักกันในนามของผู้ที่ค้นพบ
วิธีการแจงกรณี ซึ่งทำให้สามารถคำนวณหาพื้นที่และปริมาตรได้
อาร์คิมิดีส ได้พัฒนาวิธีการนี้ต่อ และได้พัฒนาวิธีการช่วยคำนวณ ซึ่งคล้ายคลึงกับแนวคิดในปัจจุบันด้วย
ไลบ์นิซ และ
นิวตัน มักจะได้รับการยอมรับว่าเป็นผู้ที่คิดค้นแคลคูลัสขึ้นมา โดยเฉพาะการค้นพบทฤษฎีบทมูลฐานของแคลคูลัส
มีการโต้เถียงกันว่านิวตันหรือไลบ์นิซ ที่เป็นผู้ที่ค้นพบแนวคิดหลักของแคลคูลัสก่อน ความจริงนั้นไม่มีใครรู้ได้ สิ่งที่ยิ่งใหญ่ที่สุด ที่ไลบ์นิซได้พัฒนาให้กับแคลคูลัส คือ เครื่องหมายของเขา เขามักจะใช้เวลาเป็นวัน ๆ นั่งคิดถึงสัญลักษณ์ที่เหมาะสม ที่จะแทนที่แนวคิดทางคณิตศาสตร์ อย่างไรก็ตาม การโต้เถียงกันระหว่างไลบ์นิซ และนิวตัน ได้แบ่งแยกนักคณิตศาสตร์ที่พูดภาษาอังกฤษ ออกจากนักคณิตศาสตร์ในยุโรป เป็นเวลานานหลายปี ซึ่งทำให้คณิตศาสตร์ในอังกฤษล้าหลังกว่ายุโรปเป็นเวลานาน เครื่องหมายที่นิวตันใช้นั้น คล่องตัวน้อยกว่าของไลบ์นิซอย่างเห็นได้ชัด แต่ก็ยังใช้กันในอังกฤษจน
Analytical Society ได้ใช้เครื่องหมายของไลบ์นิซในศตวรรษที่ 19 ตอนต้น สันนิษฐานกันว่า นิวตันค้นพบแนวคิดเกี่ยวกับแคลคูลัสก่อน แต่อย่างไรก็ตาม ไลบ์นิซเป็นผู้ที่เผยแพร่ก่อน ทุกวันนี้เป็นที่เชื่อกันว่า ทั้งนิวตันและไลบ์นิซต่างก็ค้นพบแคลคูลัสด้วยตนเอง
ผู้ที่ได้ชื่อว่าเป็นผู้พัฒนาวิชาแคลคูลัสนอกจากนี้คือ
เดส์การตส์,
Barrow,
เดอ แฟร์มาต์,
ฮอยเก้นส์ และ
วอลลิสโดยเฉพาะ เดอ แฟร์มาต์ ซึ่งบางครั้งได้รับการยกย่องว่าเป็น บิดาแห่งแคลคูลัสเชิงอนุพันธ์. นักคณิตศาสตร์ชาวญี่ปุ่น
โควะ เซกิ ซึ่งมีชีวิตอยู่ในช่วงเวลาเดียวกันกับ ไลบ์นิซ และนิวตัน ได้ค้นพบหลักการพื้นฐานบางอย่างเกี่ยวกับ แคลคูลัสเชิงปริพันธ์ แต่เขาไม่เป็นที่รู้จักในโลกตะวันตกในขณะนั้น และเขาก็ไม่ได้ติดต่อกับนักวิชาการชาวตะวันตกเลย
แคลคูลัสเชิงอนุพันธ์
อนุพันธ์ (derivative) คือการหาค่าความเปลี่ยนแปลงของตัวแปรหนึ่ง เมื่ออีกตัวแปรหนึ่งเปลี่ยนแปลงในปริมาณที่น้อยมากๆ บางทีอนุพันธ์ที่เราจะได้พบครั้งแรกในโรงเรียนคือ สูตร
อัตราเร็ว = ระยะทาง/เวลา สำหรับวัตถุที่เคลื่อนที่ด้วยอัตราเร็วคงที่ อัตราเร็วของคุณซึ่งเป็นอนุพันธ์ที่บอกการเปลี่ยนแปลงตำแหน่งในระยะเวลาหนึ่ง วิชาแคลคูลัสพัฒนาขึ้น เพื่อจัดการกับปัญหาที่ซับซ้อนและเป็นธรรมชาติกว่านี้ ซึ่งอัตราเร็วของคุณอาจเปลี่ยนแปลงได้
อนุพันธ์ของฟังก์ชัน กล่าวถึงกราฟของฟังก์ชันนั้นในช่วงสั้น ๆ ซึ่งทำให้เราสามารถหาจุดสูงสุด และจุดต่ำสุด ของฟังก์ชันได้ เพราะว่าที่จุดเหล่านั้นกราฟจะขนานกับแกนราบ ดิเฟอเรนเชียล แคลคูลัสยังมีการประยุกต์ใช้อื่นๆอีก เช่น
ระเบียบวิธีของนิวตัน (Newton's Method) ซึ่งเป็นวิธีในการหาค่ารากของฟังก์ชัน โดยการประมาณค่าโดยเส้นสัมผัส ดังนั้นแคลคูลัสเชิงอนุพันธ์ จึงสามารถนำไปประยุกต์ใช้กับหลากหลายคำถาม ซึ่งถ้ามองแค่ผิวเผินอาจคิดว่า ไม่อาจใช้แคลคูลัสจัดการได้
แคลคูลัสเชิงปริพันธ์
แคลคูลัสเชิงปริพันธ์ศึกษาวิธีการหา
ปริพันธ์ (อินทิกรัล, Integral) ของฟังก์ชัน ซึ่งอาจนิยามจากลิมิตของผลรวมของพจน์ (ซึ่งเรียกว่าลิมิตของผลรวมรีมันน์) แต่ละพจน์นั้นคือพื้นที่ที่เป็นสี่เหลี่ยมผืนผ้าแต่ละแถบใต้กราฟของฟังก์ชัน ทำให้การอินทิเกรตเป็นวิธีที่ได้ผลวิธีหนึ่งในการหาพื้นที่ใต้กราฟ และ
พื้นที่ผิว และ
ปริมาตรของแข็งเช่น
ทรงกลมและ
ทรงกระบอก
พื้นฐานของแคลคูลัส
ทฤษฎีบทมูลฐานของแคลคูลัส เบื้องต้น
ทฤษฎีบทมูลฐานของแคลคูลัสกล่าวว่า การหา
อนุพันธ์และการหาปริพันธ์เป็นวิธีการที่ตรงกันข้ามกัน กล่าวคือ ถ้าเราสร้างฟังก์ชันที่เป็นปริพันธ์ของฟังก์ชันหนึ่งขี้นมา อนุพันธ์ของฟังก์ชันที่เราสร้าง ก็จะเท่ากับฟังก์ชันนั้น นอกจากนี้ เรายังหาปริพันธ์จำกัดเขตได้ด้วยการกำหนดค่าให้กับปฏิยานุพันธ์
ทฤษฎีบทมูลฐานของแคลคูลัสเขียนในรูปสัญลักษณ์คณิตศาสตร์ได้ดังนี้: ถ้า f เป็นฟังก์ชันที่มีความต่อเนื่องบนช่วง [a, b] และ F เป็นปฏิยานุพันธ์ของ f บนช่วง [a, b] แล้ว
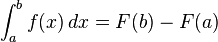
- และสำหรับทุก x ในช่วง [a, b] จะได้ว่า

ความจริงข้อนี้ปรากฏแก่ทั้ง
นิวตัน และ
ไลบ์นิซ ซึ่งเป็นกุญแจนำไปสู่ การขยายผลลัพธ์เชิงวิเคราะห์อย่างมากมายหลังจากงานของทั้งสองเป็นที่รู้จัก. ความเชื่อมโยงนี้ ทำให้เราสามารถย้อนความเปลี่ยนแปลงทั้งหมดในฟังก์ชันในช่วงหนึ่ง จากอัตราการเปลี่ยนแปลงในขณะใดขณะหนึ่ง โดยการหาปริพันธ์ของส่วนหลัง. ทฤษฎีบทมูลฐานนี้ยังให้วิธีในการคำนวณหา ปริพันธ์จำกัดเขต ด้วยวิธีทางพีชคณิตเป็นจำนวนมาก โดยไม่ต้องใช้วิธีการหา
ลิมิต ด้วยการหา
ปฏิยานุพันธ์. ทฤษฎีบทนี้ยังอนุญาตให้เราแก้
สมการเชิงอนุพันธ์ ซึ่งคือสมการที่เกี่ยวข้องกันระหว่าง ฟังก์ชันที่ไม่ทราบค่า และอนุพันธ์ของมัน. สมการเชิงอนุพันธ์นั้นมีอยู่ทั่วไปในวิทยาศาสตร์
การประยุกต์นำมาใช้
การพัฒนาและการใช้แคลคูลัสได้ขยายผลไปแทบทุกส่วนของการใช้ชีวิตในยุคใหม่ มันเป็นพื้นฐานของ
วิทยาศาสตร์เกือบทุกสาขาโดยเฉพาะ
ฟิสิกส์ การพัฒนาสมัยใหม่เกือบทั้งหมด เช่น เทคนิค
การก่อสร้าง การบิน และ
เทคโนโลยีอื่น ๆ เกือบทั้งหมด มีพื้นฐานมาจากแคลคูลัส
ดูเพิ่ม